業界初 建物における音響・振動解析の新計算手法を実用化
迅速かつ高精度に予測し、遮音性能を最適評価
2019年10月2日
大成建設株式会社
大成建設株式会社(社長:村田誉之)は、建設業界で初めて鉄筋コンクリート造の建物に生じる音響・振動を効率よく解析する新たな計算手法を実用化しました。本計算手法を用いることにより、従来の手法と比較して、計算に要するメモリ容量や時間が大幅に削減され、複雑な形状の建物の音響・振動を迅速かつ高精度に予測することができます。
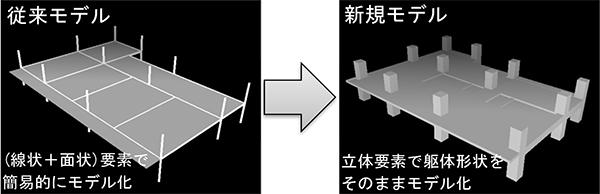
これまで建物を伝わる音響や振動の予測は、通常、梁や柱を「線状」、床を「面状」の要素(メッシュ)に置き換えてモデル化し、数値計算手法の一つである「有限要素法(以下、FEM)」※1を用いて解析を行ってきました。しかし、このモデルは実際の躯体形状を正確に再現するものではなく、簡易的なモデルのため、計算精度には限界がありました。一方、躯体形状を正確にモデル化した「立体メッシュ」を用いた場合、線状・面状メッシュによる解析に比べて、計算精度は高くなるものの、入力情報量の増大に伴い、メモリ容量の増加や計算に時間を要することから、これまで建物の音響・振動を迅速に予測することは困難でした。
そこで当社は、すでに地球物理学分野で大規模な地震動解析などに利用されている高精度の計算手法『hp-有限要素法(以下、hp-FEM)』※2に着目し、この計算手法を建物の音響・振動予測を迅速かつ高精度に行える形式に改良し、建設業界で初めて実用化しました。
本計算手法の特徴は以下のとおりです。
- 1複雑な躯体形状を自動でモデル化
従来のhp-FEMは、隣り合う要素間の面の大きさや形状を同じに揃える必要があり、自由な形状でのモデル化が困難でした。そこで、面の大きさや形状の異なる要素でも連続して扱える非適合要素※3を組み込むことで複雑な形状にも対応でき、かつモデル作成を自動化し、モデル化を容易に行えるようにしました。 - 2迅速で、高精度な音響・振動予測を実現
本計算手法を適用することで、従来のFEMと比較してメモリ容量と計算時間を各々約半分程度に抑えながら同等の計算精度が得られます。(図1参照)一例として集合住宅躯体の一部(延床面積約400m2)をモデル化して複数パターンで床衝撃音を予測した場合、従来は計算に数日を要しましたが、本手法では1日程度で完了しました。また立体メッシュを用いて建物を忠実にモデル化することから高精度な音響・振動予測が可能となります。 - 3予測精度向上により、最適な躯体構造を選定可能
音響・振動の予測精度が向上するため、建物の遮音性能を考慮した最適な躯体構造を選定することができるなど、より自由度の高い設計が可能となります。 - 4床衝撃音を高精度に予測し、躯体の遮音性能を評価
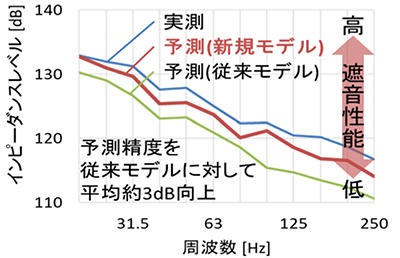
建物で生じる床衝撃音の予測にも応用でき、建物を立体メッシュにより忠実にモデル化し、特に梁や柱の近傍での遮音性能の予測精度向上が可能となります(図2、3参照)。
今後、当社は、建物内を伝搬する様々な音響・振動の予測について、開発済の重量床衝撃音予測システム「TSounds-Floor」をはじめとする音響・振動解析にも本計算手法を用いることで、更にその予測精度を向上させてまいります。
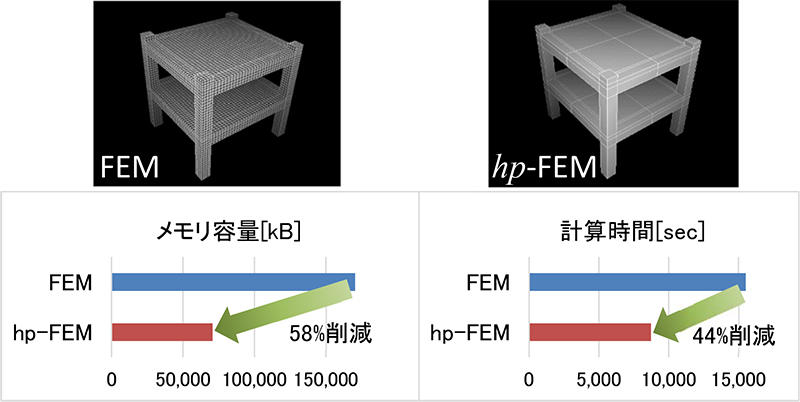
(床衝撃音実験室における予測計算時のメッシュ分割状況、メモリ容量、計算時間)
- ※1有限要素法:対象を細かい要素(メッシュ)に分割し、数値解析する手法。通常、解析対象の幾何学的特徴によって分割する要素の種類が使い分けられ、線状要素、面状要素、立体要素の順に解析精度は高くなるが、同時に計算に要する情報量の増加に伴いメモリ容量と計算時間が増大し、計算コストが高くなる。
- ※2hp-有限要素法:通常の有限要素法が一般的に要素を細かくすることで解析精度を向上させるのに対して、要素の大きさを細かくすることに加えて、要素内の任意の点で生じる応力や変位などの物理量の解析精度を高めることで効率的に解析領域全体の精度を向上させる手法。地球物理学の分野で大規模な地震動などの問題を解く際に利用されている。
- ※3非適合要素:通常のメッシュは、隣り合う要素間の面の大きさと形状が揃っていなければならないが、非適合要素は、面の大きさと形状の異なる要素間でも、応力や変位などを連続的に取り扱うための複数方程式を連立して解くような数学的な処理を施すことで、要素同士を結合することができる。通常のメッシュに比べて形状に対する柔軟性が高く、自由な形状でのモデル化が可能となる。
